2014 m. rugpjūčio pirmąją dieną, paskutinę dieną kaimo turizmo sodyboje, man pagaliau nusišypsojo žvejiška laimė. Užkibo „dvikilograminis“ karšis. Dvikilograminiu jį pakrikštijome su vaikais dar iš vandens neištraukę. Na taip, jis buvo aiškiai daug didesnis už tuos, kuriuos buvo tekę pagauti anksčiau.
Tačiau iškart ištiko bėda. Ne ne, karšis nepabėgo. 🙂 Štai įrodymas:

Bėda buvo ta, kad neturėjau nei kuo karšį pamatuoti, nei kuo pasverti. Svarstyklių neatsirado ir visoj kaimo turizmo sodyboj „Pas Algirdą“. Jei vietoje liniuotės sugalvojau panaudoti siūlą (kurį išmatavus vėliau išaiškėjo, jog karšis buvo 54 cm ilgio), tai jo tikslus svoris taip ir liko nežinia, nes karšį išsikepėme ir suvalgėme tą patį vakarą.
Žinant visus anekdotus apie žvejus, perdedančius žuvų dydį, nesijausdavau labai užtikrintai pasakodamas apie šį, patį didžiausią savo gyvenime laimikį. Bet jei tikslių duomenų ir nėra, tai kam tada reikalinga statistika? Štai ir nusprendžiau pamėginti paskaičiuoti galimą to karšio dydį pasinaudodamas statistikos programa R.
Visų pirma, iš Kimba.lt svetainės ir iš savo šaldytuvo susirankiojau duomenis apie karšių ilgius ir svorius. Nedaug tepavyko rasti. Radau dešimt laimikių, kurių sąvininkai nepatingėjo ir išmatuoti, ir pasverti:
Ilgis Svoris Komentaras 30 0,50 //kimba.lt/zvejyba/laimikis/perziura/108?s=l 34 0,65 //kimba.lt/zvejyba/laimikis/perziura/708?s=l 42 0,68 //kimba.lt/zvejyba/laimikis/perziura/612?s=l 41 0,84 Šaldytuve esantis karšis :) 40 1,00 //kimba.lt/zvejyba/laimikis/perziura/187?s=l 45 1,89 //kimba.lt/zvejyba/laimikis/perziura/1028?s=l 60 2,40 //kimba.lt/zvejyba/laimikis/perziura/391?s=l 70 2,50 //kimba.lt/zvejyba/laimikis/perziura/873?s=l 60 2,78 //kimba.lt/zvejyba/laimikis/perziura/325?s=l 60 2,80 //kimba.lt/zvejyba/laimikis/perziura/1155?s=l 47 3,20 //kimba.lt/zvejyba/laimikis/perziura/283?s=l 65 3,83 //kimba.lt/zvejyba/laimikis/perziura/408?s=l
Atvejo, kad karšis būtų +-54 cm ilgio neradau. Ką gi, teks daryti statistines prielaidas remiantis kitais duomenimis.
Labai panašius skaičiavimus į tuos, kuriuos pats ketinau atlikti, radau knygoje „R In Action“, 179-181 psl. (Beje, tai puikus R vadovėlis.)
Šiuos duomenis importavau į RKward (R grafinės sąsajos) programos „data frame“ tipo objektą. Ir padariau duomenų sklaidos grafiką:
> plot(karsiai$Ilgis,karsiai$Svoris,
xlab="Ilgis (centimetrais)",
ylab="Svoris (kilogramais)")
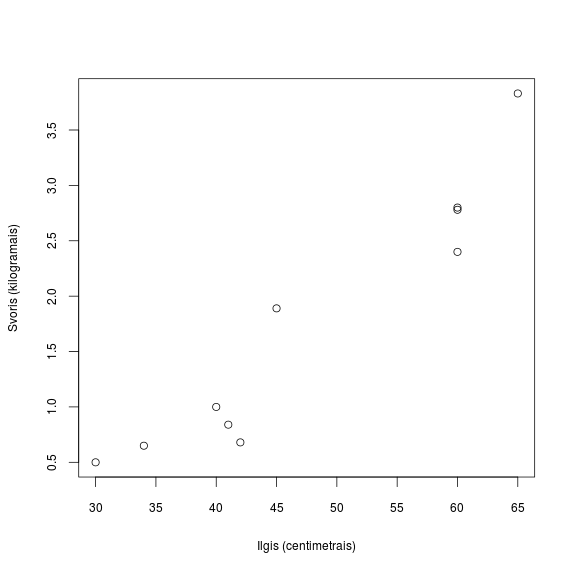
Na, paėmus liniuotę ir nubrėžus labiausiai tikėtiną tiesinės priklausomybės tarp karšio svorio ir ūgio liniją jau galima matyti, 54 cm ilgio karšis vidutiniškai bus didesnis nei 2 kg. Valio!
Tačiau čia nesustokime, pritaikykime duomenims tiesinę regresiją (nes iš pirmo žvilgsnio neatrodo, kad priklausomybės linija būtinai turi būti lenkta).
> modelis <- lm(Svoris ~ Ilgis, data=karsiai)
> summary(modelis)
Call:
lm(formula = Svoris ~ Ilgis, data = karsiai)
Residuals:
Min 1Q Median 3Q Max
-0.5500 -0.2389 -0.0410 0.2858 0.5543
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -2.50557 0.50436 -4.968 0.0011 **
Ilgis 0.08894 0.01026 8.666 2.44e-05 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.3837 on 8 degrees of freedom
Multiple R-squared: 0.9037, Adjusted R-squared: 0.8917
F-statistic: 75.11 on 1 and 8 DF, p-value: 2.444e-05
Iš aukščiau pateiktų skaičiavimų, „Coefficients“ lentelės matyti, kad karšio ilgio centimetras prideda 0.089 kg (89 g) svorio. „Intercept“ parametro minusinės reikšmės (-2.506) nereikėtų priimti kaip prasmingo taško – šiaip ar taip, 0 cm ir 0 kg karšių nebūna, o mūsų duomenyse mažiausias karšis – 30 cm ilgio. Koeficientų lentelės „Pr(>|t|)“ stulpelyje „Ilgis“ eilutėje nurodoma, kad regresijos koeficientas yra reikšmingai besiskiriantis nuo nulio (p < 0,001). Parametras „Multiple R-squared“ – 0.9037 – rodo, kad modelis paaiškina atitinkamo ilgio karšių 90% svorio variacijų (tai netgi daug, sakyčiau. Juk žuvis – gyvas sutvėrimas, jos svoris priklauso ir nuo vandens telkinio, ir nuo metų laiko, ir kitų faktorių).
Taigi, gauname formulę, kaip paskaičiuoti karšio svorį:
svoris = -2,506 + 0,089 * ilgis
Jei karšio ilgis buvo 54 cm, tai:
-2.506 + 0,089 * 54 = 2,3 kg
Taigi, puiku! Aš neapsimelavau sakydamas, kad mano karšis svėrė 2 kg! Jis greičiausiai svėrė net daugiau.
Žinoma, ne visi tokio ilgio karšiai svers tiek pat. Kokia tikimybė, kad mano karšis bus, sakykime, lengvesnis nei 2 kg? Ne itin didelė. Paskaičiavus rezidualų standartinį nuokrypį
> residuals(modelis)
1 2 3 4 5 6 7 8 9 10
0.337 0.132 -0.550 -0.301 -0.052 0.393 -0.431 -0.051 -0.031 0.554
> sd(residuals(modelis))
[1] 0.3617976
matome, kad standartinis nuokrypis – O,362 kg., kas, nesigilinant į detales, reiškia, kad yra tik 16% tikimybė, kad 54 cm karšis svers mažiau nei 1,94 kg (lygiai tokia pati tikimybė, kad jis svers daugiau nei 2.66 kg).
Ir galiausiai, nubrėžkime tą geriausio atitikmens liniją:
> abline(modelis)
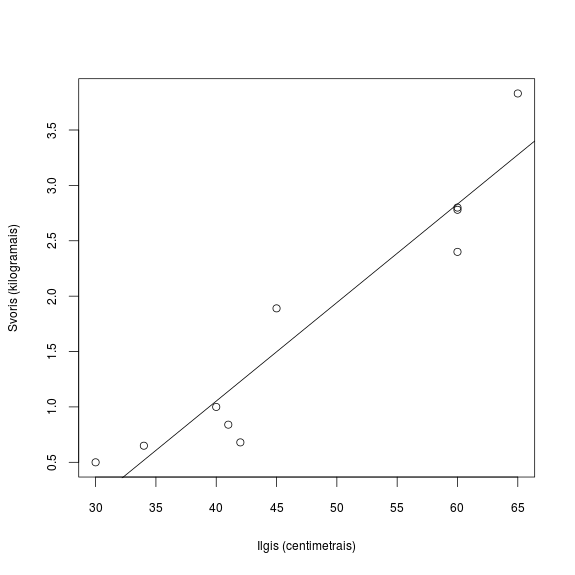
Turint daugiau duomenų būtų galima galvoti, kad ryšys tarp karšio svorio ir ilgio nebūtinai yra tiesinis. Tačiau 10 vienetų tikrai neužtenka tokiems eksperimentams.
Bet kuriuo atveju, dabar besigirdamas savo žvejybos laimikiais galiu ramia sąžine nurodyti didžiausią karšį – 2,3 kg. Ir dar: statistika gali būti naudinga ne vien sausame moksle.

Parašykite komentarą